關於「推論統計」與「無罪推論」：法院判決的類比

◎陳光輝／國立中正大學政治學系副教授

不時聽聞司法案件的判決，讓社會上很多人覺得不滿，認為又是「恐龍法官」的錯。事後的評論者陸續提到「無罪推論」這個原則。這令人聯想到，「無罪推論」原則與推論統計「假設檢定」中的「虛無假設」有著相似性。大學部統計方法課程，到了假設檢定這個單元時，台下的年輕同胞們，常覺得困惑。在這裡，我們將「假設檢定」與司法審判過程做個連結，試圖理解法官如何由無罪推論出發，判定被控告者是否有罪。¹

 

圖片：我國司法院憲法法庭。來源：C.C. by Jiang。

推論統計的原理

先說明一下，什麼叫做推論統計（inferential statistics）。我們常常對於特定對象的某些狀況感到好奇。這個特定對象，我們稱為母群體（population）。我們將母群體裡特定狀況的真正數值稱為母體參數（population parameter），這個特定狀況可能指涉單一個現象，是一個變數，也可能是不同現象或變數間的關係，也就是變數間的關連程度。

現實的狀況是，我們通常不知道母體參數的正確值為何。所以，我們會以隨機抽樣的方式從這個母群體裡抽出數量較小的一群個體，稱為樣本（sample），瞭解他們在這個變數上的狀況，得到樣本在這個變數上的數值，稱為樣本估計值（sample statistic）。接著根據這個樣本估計值，我們來推論母群體在這個變數上的真正值(母體參數)為何，這就是推論統計。例如，我想知道在鳳梨田大學的學生平均一年吃了幾顆鳳梨？或是，吃的鳳梨數量跟體重之間有沒有關係？這樣的問題是存有真實的答案，這就是母體參數。問題是，我們不知道這個數值為何，所以，我們抽取了一組具有代表性的學生，正確測量了他們每個人每年吃了幾顆鳳梨，得到了一個平均數，做為樣本估計值，來推論真正的答案可能為何。

假設檢定的目的是針對我們提出的一個假設，依據我們所得到的樣本估計值來推論母體參數的真實值，決並定是否拒絕這個假設。這個過程跟法官針對一個司法案件進行審判，決定被告是否有罪一樣。針對單一個變數進行估計時，我們假設母體參數為一個特定值，例如，我們想知道鳳梨田大學的年輕人每年吃了幾顆鳳梨（這邊我們先假設一年吃了2.5顆），以及想要解釋是什麼因素讓某些人吃多一點鳳梨或吃少一點鳳梨。在討論幾個「變數」之間關係時，這個母體參數通常被假設為0，或是「變數間沒有關係存在」，例如，我們想知道「體重」跟吃幾顆鳳梨有沒有關係、想要做研究來檢視一下是不是體重愈重的人吃愈多鳳梨，我們會先假設吃鳳梨跟體重沒有關係。上面這兩種假設，我們稱為虛無假設（null hypothesis）。這就像是司法審判裡的無罪推論：我們預設被告是無罪的，是沒有做這個犯罪行為的。

 

圖片來源：C.C. by Fukuzawa。

 

進行假設檢定時，什麼狀況才能去推翻這個虛無假設？我們在這裡用「平均數」的概念來進行理解。如果得到的樣本估計值跟我們假設的母體參數，相距不遠，我們會覺得這個差距有可能是抽樣誤差導致的結果。意思是說，因為我們手上有的是樣本資料，每次抽樣結果多少會有些不同，所以會有誤差存在。就算我們的虛無假設是正確的，樣本估計值也不會剛好等於母體參數。因此，當樣本估計值與假設的母體參數之間差異不大，我們不會說這個虛無假設不對，我們就不拒絕這個虛無假設。當樣本估計值跟母體參數差距夠大了，我們就會說，這個虛無假設應該是不對的，我們就做出拒絕虛無假設的結論。簡單說來，我們有一個虛無假設，就看由樣本得到的估計值跟這個虛無假設差多遠，如果夠遠，我們覺得被說服了，就會拒絕虛無假設，說：真實的母體參數不等於我們說的那個特定值。

至於多遠才叫遠？我們會設一個標準，通常是設在我們相信我們至少有95％的把握，相信我們的結論是對的，這個叫做信心水準（confidence level）。相對而言，最多有5％的機會，我們的結論是錯誤的。我們的樣本估計值跟虛無假設裡的母體參數，差得越遠，我們就越有把握拒絕虛無假設是對的。這麼做的基礎在哪裡？有個定理叫做中央極限定理（central limit theorem）來支持我們。很簡單的說法是：我們每次抽一樣多的樣本，會得到一個平均值，抽了很多很多次之後，這些樣本平均值放在一起會形成一個常態分配；此外，在個常態分配裡，這些樣本平均數的平均數會正好等於母體平均數（就是母體參數），標準差會等於母體標準差除於樣本數開跟號之值。

我們先說明什麼是常態分配，它是一個鐘形對稱的分配，若一個變數呈現常態分配，我們就可以計算，某個區段的數值發生的可能性有多高。例如，同學們吃掉的鳳梨數成呈常態分配，有人吃得多，有人吃的少，平均數為2.5，標準差為1.3，我們可以知道有64.97%的同學吃了兩顆以上，有35.03%的同學吃了兩顆以下（請見圖一），或是，前四分之一的人至少吃了3.38顆鳳梨（請見圖二）。

 

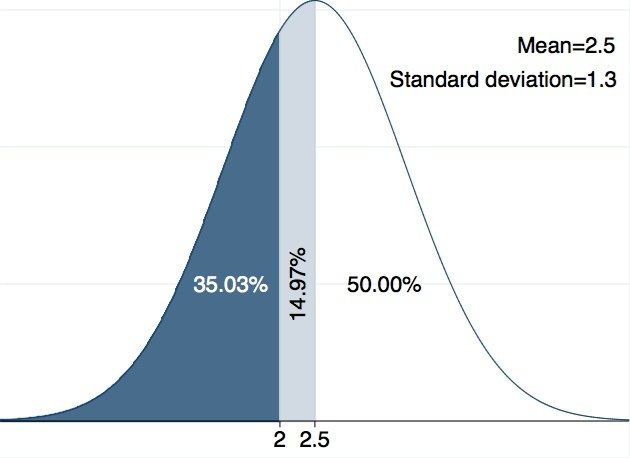
圖一：常態分佈圖。來源：作者自製。

 

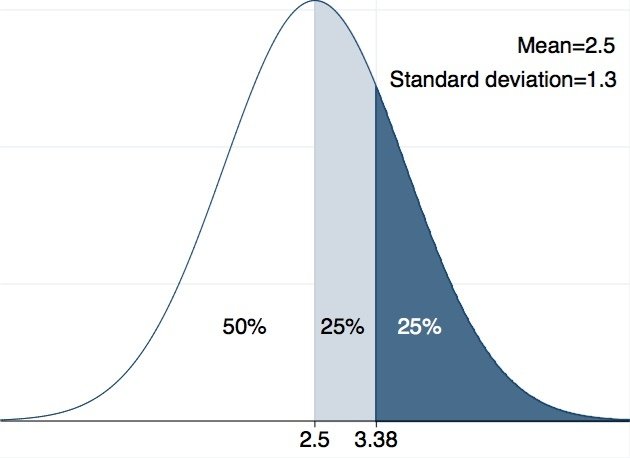
圖二：常態分佈圖。來源：作者自製。

 

我們再回到上一段所說的虛無假設的檢定。根據中央極限定理，重複抽樣所得到的所有樣本平均數們會形成一個常態分配，我們手中這套樣本的平均數是當中的一個值。因此，我們可以得出多遠是超過95％的標準，通常就是以常態分配的中心點為中心，左右各47.5％的地方為界線。如果我們的虛無假設的母體參數是對的，有95％的機會，我們的樣本平均數會落在這個範圍內。這樣的狀況下，我們會認為這個虛無假設應該是合理的。反之，如果虛無假設是對的，但樣本估計值卻落在這個界線之外，發生這樣狀況的機率很低（只有5％），是不太合理的狀況，我們就會拒絕這個虛無假設。這左右2.5％的區域，我們稱為拒絕域（請見圖三）。當我們的樣本估計值落在拒絕域時，我們有超過九成五的把握說拒絕這個虛無假設是對的。反之，我們有不到5％的機會做了錯誤的結論：虛無假設是對的，我們卻說它是錯的。

 

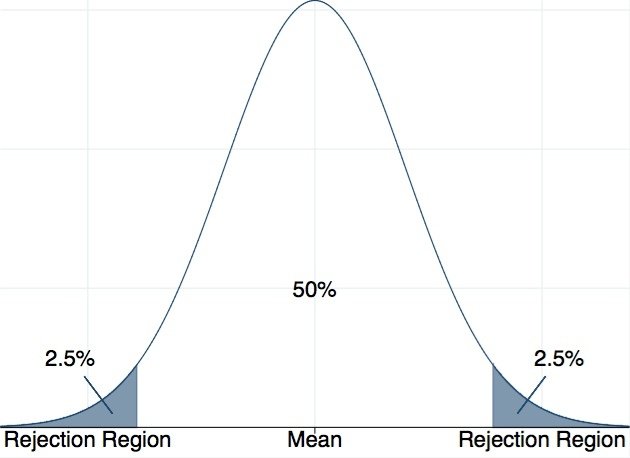
圖三：拒絕域。來源：作者自製。

 

司法審判與無罪推論

換句話說，當我們得到的樣本資料距離我們的虛無假設所說的母體參數值夠遠，我們就可以被說服說這個虛無假設是錯的。好，回到司法審判，一開始，我們就接受無罪推論，我們由相信這個被告是無罪的這個點出發。這個點，就像是上面假設檢定裡說的虛無假設。我們相信被告是無罪，這就是我們假設的母體參數。接著，就由檢察官提出證據，來告訴法官實際的狀況是如何。同時，這些證據也要接受辯護律師的檢視跟質疑。如果這些證據具有說服力，就可以將法官由相信被告是無罪的這個虛無假設，往相信這個人是有罪的方向拉。越有說服力的證據，就可以將法官拉得更遠。同時，辯護律師也提出有利於被告的證據來把法官往回拉。如果，檢察官的證據把法官往有罪方向拉得夠遠，而辯護律師提供的證據無法將法官往回拉，就像我們上面說的，超過了95％的把握，法官就會判決被告有罪。反之，法官就會將被告判為無罪。

在上面的假設檢定中，我們依據具代表性的抽樣資料來決定是否拒絕虛無假設。在司法審判裡，法官依據雙方證據來決定是否要否定被告是無罪的這個虛無假設。

當近來一些的司法案件判決出來時，一陣嘩然，法官被罵爆了！因為，社會裡的多數人都相信被告是有罪的。這跟法官所應站立的立場是不同的，因為法官要站在無罪推論的立場。當然，法官在相同性質的不同個案裡，是不是都是使用同一種標準？這也是目前引起爭議的一個問題。為什麼看起來相似的案件，結果卻截然不同？一個可能的解釋是：法官的心證。同樣的資訊，不同的人可能會有不同的認知與想法，法官在判案時，可能也有如此的狀況。回到上述我們提到以95％為標準，如果樣本估計值超過這個95％的範圍，我們就拒絕虛無假設。不過，95％是一個在社會科學領域裡常被使用的標準，不同的研究者或許會使用不的標準：有人使用90％，也有時使用99％（請見圖四）。

 

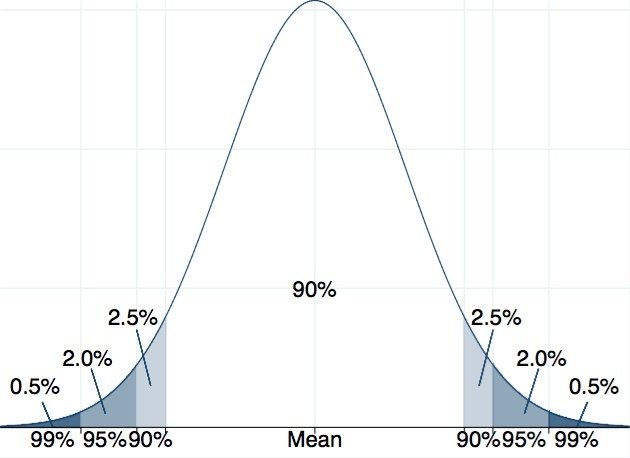
圖四：不同的信心水準，拒絕域的範圍不同。來源：作者自製。

 

使用90％時，決定是否要拒絕虛無假設的兩端界線的距離比較近，比較可能拒絕虛無假設；使用99％時，距離就比較遠，也就比較難拒絕虛無假設。所以，在一個假設檢定裡，同樣的樣本估計值，若使用不一樣的信心水準時，可能獲得不一樣的結果。相同的，同樣的案件，同樣的證據，法官的標準若不相同，結果可能就有所不同。一個採用較寬鬆的標準的法官，就像是使用90％的信心水準，比較可能接受檢察官提出的證據，否定被告是無罪的這個虛無假設。相對的，一個以較高的標準進行審判的法官，就像是使用99％的信心水準，接受檢察官證據的可能性就比較低一點。因為標準的不同，導致了判決的不同。最高的信心水準可以到多高？由我們這裡使用的常態分配來看，接近100％，但從來不會達到100％。

面對司法審判的爭議時，我們要問的是：為什麼是無罪（無罪就是虛無假設中的母體參數）？是法官的標準有問題嗎（這就是信心水準的問題）？還是檢察官提供的證據是不足的（這就是樣本估計值的問題）？在近來的一些判決爭議中，一開始，大眾質疑的是法官的標準，之後，有較多的討論，指向了是檢察官的證據是不足的。這就像是：我們拿了一筆資料，進行假設檢定，結果是我們覺得不對的。可是，這不僅可能是這個決定有問題，也有可能是我們的樣本資料有問題，導致了這樣的結果。假設檢定跟司法判決一樣，我們都必須弄清楚我們的起始點在哪裡，證據是否有足夠的說服力，我們所使用的標準是否合理。如果以假設檢定的角度來說，無論我們用了多高的標準來做決定，都不會達到100％的信心水準。司法判決似乎也有這個屬性，也難怪，我們看不到從不引起爭議的司法體系。

 

菜市場政治學延伸閱讀
〈為什麼「縣市長排名」並不能反映真實：淺談民調抽樣〉
〈對比式選舉民調的錯誤解讀〉