◎ 林澤民/美國德州大學奧斯汀分校政府系教授
※本文原發表於作者部落格,為演講內容。原文整理後已發表在《社會科學論叢》2016年10月第十卷第二期。全文請點選按此。投影片請點選按此。
〈系列1文章連結:p值是什麼〉
p值不是什麼
我本來放Magnolia「玉蘭花」這部電影都是為了在教學上解釋p值的概念,可是後來當我注意到對於p值的爭議之後,覺得其實這一部電影也可以用來幫我們了解為什麼用p值來做統計推論有可能是錯的。
下面這個表是大家都熟悉的。(圖二) 我們可以用這個表來呈現有關虛無假設是對或者不對,是被拒絕或者被接受的四種可能性,其中兩種是作出錯誤統計推論的情況。第一個情況,虛無假設是對的,但統計檢定是顯著的,因此虛無假設被推翻了。這種情況叫做Type I error,我們保留了α=0.05的機率容許它存在。第二個情況,如果虛無假設是錯誤的,但統計檢定不顯著,所以它沒有被推翻,這個情況叫做Type II error。Type II error剛學統計的同學可能不太了解,因為我們通常都不會很清楚地去計算它的機率–所謂β。這個β跟α不一樣,不是你可以用相約成俗的方法來訂定,而是會受到若干因素的影響。簡單來講,在一定的顯著水準α之下,β跟樣本大小有關係;樣本太小的話,β會比較大。另外它跟實驗效應的大小也有關係,如果效應很小的話,β也會比較大。換句話說,如果虛無假設跟研究假設的距離比較小的話,β會比較大。可是一般人不會去計算β,因為還沒做實驗之前,其實也不知道實驗的效應有多少。儘管如此,β是可以計算的。算出來了,則我們拒絕錯誤虛無假設,而作出正確統計推論的機率是1-β,這1-β我們就把它叫做「檢定的強度」–the power of the test–我待會兒會用到這個名詞。依此定義,β越小的話,power就越大。用醫學的術語來說,α,Type I error的機率,就是偽陽性的機率,而β,Type II error的機率,就是偽陰性的機率。

圖二
我們可以開始討論:傳統用p值來作統計檢定方式,為什麼有問題?剛剛ASA的聲明說:p值 do not measure the probability that the studied hypothesis is true。p值告訴你:如果虛無假設是對的,你「觀察到資料」的機率有多少,但它並沒有告訴你「虛無假設是對的」的機率有多少,或「研究假設是對的」的機率有多少。這是很不一樣的:前者是data的機率,後者是model的機率。進一步說明,p值是在虛無假設為真的條件之下,你觀察到和你所觀察到的統計值一般大小(或更大/更小)的機率。但我們作檢定的時候,我們是看p值是不是小於你的統計水準α,如果p<α,我們就說統計是顯著的。換句話說,如果虛無假設為真,那麼你的檢定是顯著的機率是α=0.05。但這其實不是我們作研究最想回答的問題;這個機率只告訴我們,如果你的虛無假設為真,有百分之五的機率,data會跟它不合,但它沒有告訴我們虛無假設這個model為真的機率有多少,而這才是我們應該問的問題。所以我們應該反過來問,如果你統計檢定是顯著的,在此條件之下,「虛無假設是對的」的機率有多少?如果我們把關於data這個偽陽性的機率記作α=Pr(Test=+|H0),大家可以看出這個關於model的機率其實是它倒反過來的:Pr(H0| Test=+),所以我把它稱作「偽陽性的反機率」。這兩個機率原則上不會相等;只有在 α=0的時候,兩者才都是零而相等。
譬如今天你去健康檢查,醫生給你做很多篩檢,如果篩檢結果是陽性,其實先不要怕,因為你應該要問,如果篩檢出來是陽性,那麼你真正並沒有病的機率是多少?也就是偽陽性的反機率有多少?大家可能會很驚訝,偽陽性的反機率通常都很高,但是這個機率,p值並沒有告訴你。所以必須要去算在檢定是陽性的條件下,結果是一種偽陽性的反機率;這就必須要用「貝式定理」來算。
雖然在座有很多可能比我更高明的貝氏統計學家,但我還是要說明一下貝式定理。先舉一個我終身難忘的例子,剛剛陳老師說我是台大電機系畢業的,我在電機系的時候修過機率這一門課。我記得當時的期中考,老師出了一個題目,說我口袋裡面有三個銅板,其中有一個銅板是有偏差的銅板,偏差的銅板它得到正面的機率是1/3–不是1/2–而得到反面的機率是2/3。考題問:現在我隨機從口袋裡面掏出一個銅板,這個銅板是那個偏差銅板的機率是多少?很簡單大家不要想太多,1/3嘛。可是我現在拿銅板丟了一下,出現的是正面,我再問你這個銅板是那個偏差銅板的機率是多少?我不期望大家立刻回答,因為要用貝式定理來算,當你獲得新的資訊的時候,新的資訊會更新原來的機率。這裡我也沒有時間詳細告訴大家怎麼算,但是可以告訴大家,結果是1/4。如果我丟擲銅板,它得到了正面,它是偏差銅板的機率變成只有1/4。這是因為偏差銅板出現正面的機率,比正常銅板要小,所以出現正面的話,它相對來講就比較不太可能是偏差的銅板,所以機率會比原來的1/3小些,只有1/4。(大家可以想像如果偏差銅板出現正面的機率是0,而丟擲得到正面,則此銅板是偏差銅板的機率當然是0。)原來所知的「1/3的機率是偏差銅板、2/3的機率是正常銅板」這個機率分配在貝氏定理中叫做先驗機率(prior probability)。大家要建立這個概念,即是還沒觀察到數據之前,對於模型的機率有一些估計,這些估計就叫做先驗機率。至於觀察到數據之後所更新的模型機率,1/4和3/4,這個機率分配叫做後驗機率(posterior probability),也就是前面所說的反機率(inverse probability)。
我們再來看另外一個跟統計檢定問題非常接近的例子。可以用剛剛身體檢查的例子,但我這裡用美國職棒大聯盟對球員的藥物檢查為例,也許比較有趣。這裡假設大約有6%的美國MLB的球員使用PED(performance enhancing drugs),這是一種可以增強體能表現的藥物,是類固醇之類的藥物。這個估計數字可能是真的,是我從網頁上抓下來的。這邊的6%即為我前面說的先驗機率:隨機選出一個球員,則他有使用PED的機率是0.06,沒有使用PED的機率是0.94。現在大聯盟的球員都要經過藥檢;舉大家熟知的火箭人Roger Clemens為例。他也是我心目中的棒球英雄,他被檢定有陽性的反應。為了方便起見,假設藥檢的準確度是95%。所謂準確度95%的定義是:如果一個球員有使用藥物,他被檢定出來呈陽性反應的機率是0.95;如果一個球員沒有使用藥物,他被檢定出來呈陰性反應的機率也是0.95。也就是我假設兩種誤差類型的機率α跟β都是 0.05。在這假設之下,使用貝式定理來計算,當球員被篩檢得到的結果是陽性,但他並不是PED使用者的後驗機率或反機率,其實高達0.45。大家可以從圖三看到貝氏定理如何可以算出這個機率。(圖三)

圖三
使用貝式定理 算出來的結果大家應該會覺得很詫異,因為我們藥物篩檢的工具應該是很準確的,0.95在我們想像中應該是很準確的,我們認為說我們錯誤的可能性只有5%,其實不然。檢定是陽性,但其實偽陽性的反機率可以高達45%!所以雖然我不是醫學專家,不過大家健康檢查,如果醫生說,你的檢查結果呈現陽性反應,大家先不要慌張,你要先問一下醫生檢驗的準確度大概有多少,如果一個真正有這種病的人來檢定,呈現偽陽性的機率有多少?如果一個沒有病的人來檢定,呈現偽陰性的機率有多少,然後再問他先驗機率大概有多少?然後自己用貝氏定理去算一下偽陽性的反機率。醫學上很多疾病,在所有人口裡面,得病的比例通常很小的。也就是說,得病的先驗機率通常都很小,所以偽陽性的反機率會很大。
現在換成了統計檢定,看下圖的表格。(圖四) 這表格跟圖三的表格很像,只是把內容改成了圖二的內容:虛無假設是真的、或是假的,然後統計檢定是顯著、或是不顯著的。然後再加上一行先驗機率,就是「虛無假設是對的」的先驗機率有多少、「虛無假設是錯的」的先驗機率有多少,都用符號來代替數目。我們可以用貝式理得到一個公式,顯示偽陽性的反機率是統計水準α、檢定強度(power=1-β)、和研究假設之先驗機率(P(HA))的函數。α跟檢定強度都沒問題,但公式裡頭用到先驗機率。你會問:在統計檢定裡面,先驗機率是什麼?

圖四
在此我必須要稍微說明一下,先驗機率,以淺白的話來講,跟你的理論有關係,怎麼說呢?如同剛剛提到ESP的實驗,好像只要就這樣用力去猜,你猜對的可能性就會比較高。發表這樣子的實驗報告,我們有沒有辦法告訴讀者,當受測者這樣皺著眉頭去想的時候,到底是什麼樣的一個因果機制,能夠去猜到圖片是出現在左邊還是右邊。
一般來說這種ESP的實驗,是沒有這種理論的,是在完全沒有理論的條件之下來做實驗。在此情況之下,我們可以說,此研究假設的先驗機率很小很小。當然我們作政治學的研究就不一樣,我們可能引用很多前人的著作,都有一個文獻回顧,我們也引用很多理論,然後我們說:我們的研究假設是很有可能展的。假如你有很好的理論,你的研究假設的先驗機率就會比較高,在這種情況之下,問題會比較小。但是還有一個問題,就是如果從文獻裡面來建立理論,來判定你的研究假設的先驗機率有多少,問題出在於:通常文獻回顧是從學術期刊裡面得來,而現在所有的學術期刊,發表的都是顯著的結果,不顯著的結果通通都沒有發表,從學術期刊上來判斷研究假設的先驗機率有多少,這樣的判斷是有偏差的。這是我今天要講的第二個問題,現在先繼續討論偽陽性反機率的問題。
現在要詳細討論影響偽陽性反機率的因素,就是影響到「統計檢定是顯著的條件之下,虛無假設為真」這一個機率的因素。這裡再重覆一下,我們一般了解的統計推論,奠基於虛無假設為真時,p值顯著的機率,也就是偽陽性的機率被控制在α之內:Pr(Test=+|H0)=Pr(p<α|H0) =α。但我們現在要反過來問的是:統計檢定是顯著的情況下,H0為真的機率,也就是偽陽性的反機率:Pr(H0| Test=+)=Pr(H0| p<α),這好比篩檢結果為陽性、但其實球員並未使用PED、患者其實無病的機率。如果α等於零,可以很清楚的發現,這兩個機率是一樣的,都是零;但α不等於零的時候,它們就不一樣。由下圖來看,偽陽性的反機率跟先驗機率–研究假設的先驗機率–以及檢驗的強度有關。(圖五、六)看圖可以得知,power越大,還有先驗機率越大的話,偽陽性的反機率就越小。可是當power越小的時候,還有先驗機率越小的時候,偽陽性的反機率就越大。
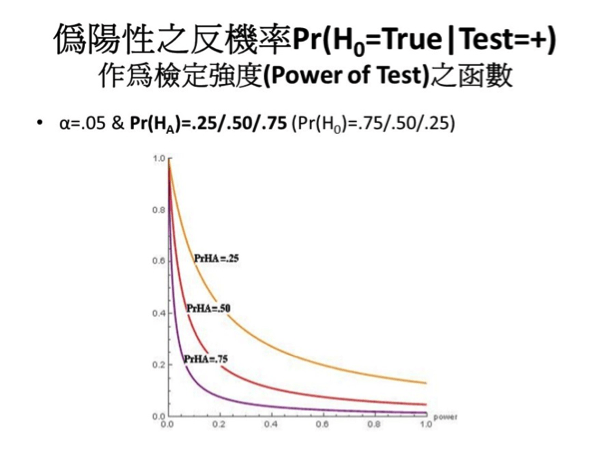
圖五
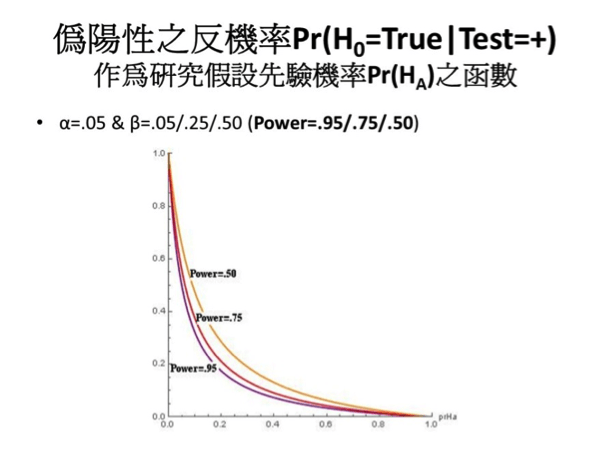
圖六
我做了一個表,列出研究假設的先驗機率,從最小排列到最大,可以看到在不同檢定強度之下,偽陽性的反機率是多少。(圖七)它可以高到近乎1.00。換句話說,研究假設的先驗機率如果很小很小,則即使p值檢定顯著,但虛無假設仍然為真的機率其實還是很大很大的。如果研究假設的先驗機率是0.5–你事先也許不知道哪一個是對的,你假設是0.5,就像丟銅板一樣,此時,偽陽性的反機率才是 0.05,才跟α一樣。也就是說,研究假設的先驗機率必須要高於0.5,偽陽性的反機率才會小於0.05。可是假如你的研究假設,譬如剛剛提到的ESP研究,這種實驗沒有什麼理論、沒有什麼因果關係,然後你就去做了一個統計分析。換句話說這個研究假設的先驗機率可能很低,此時偽陽性的反機率其實是很高的。圖七第一欄是假設power為 0.95,如果power低一點到0.75呢?如果是0.50呢?我們可以看到其實結果差不多。當然power越低,問題會越嚴重,但其實差不多,當你的先驗機率是0.5的時候,原來是 0.05,現在是 0.09,所以差別不是特別大。原則上,power對於偽陽性反機率的作用不是那麼強,作用強的是prior,即是研究假設的先驗機率。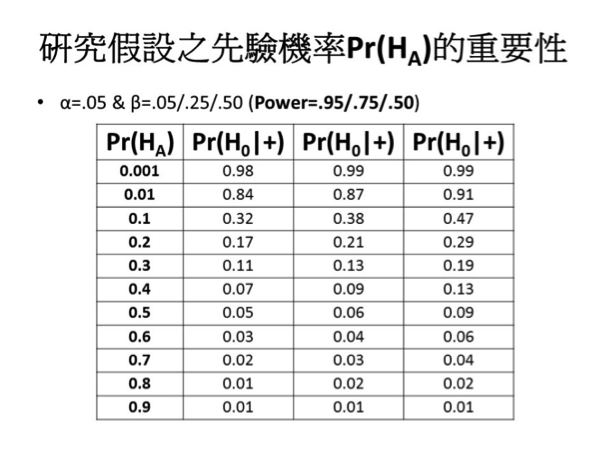
圖七
小結:當檢定強度或研究假設的先驗機率甚低的時候,α=0.05可能嚴重低估了偽陽性之反機率,也就是在p值檢定顯著的情況下,虛無假設H0仍然極有可能為真,而其為真的條件機率可能甚大於α。此時如果我們拒絕虛無假設,便作出了錯誤的統計推論。
〈系列1文章連結:p值是什麼〉
〈系列3文章連結:「摘櫻桃」問題〉
